10等于9.999……吗？

2019-12-02

这两天看到一个有趣的视频，博主Mathologer尝试证明10等于9.999……的无限循环，视频地址在YouTube。这里记录下他的证明过程，并且补充一下我自己的想法。

基础证明

因为10 / 3等于3.333……，那么两边同乘3，就可以得到10 = 9.999……

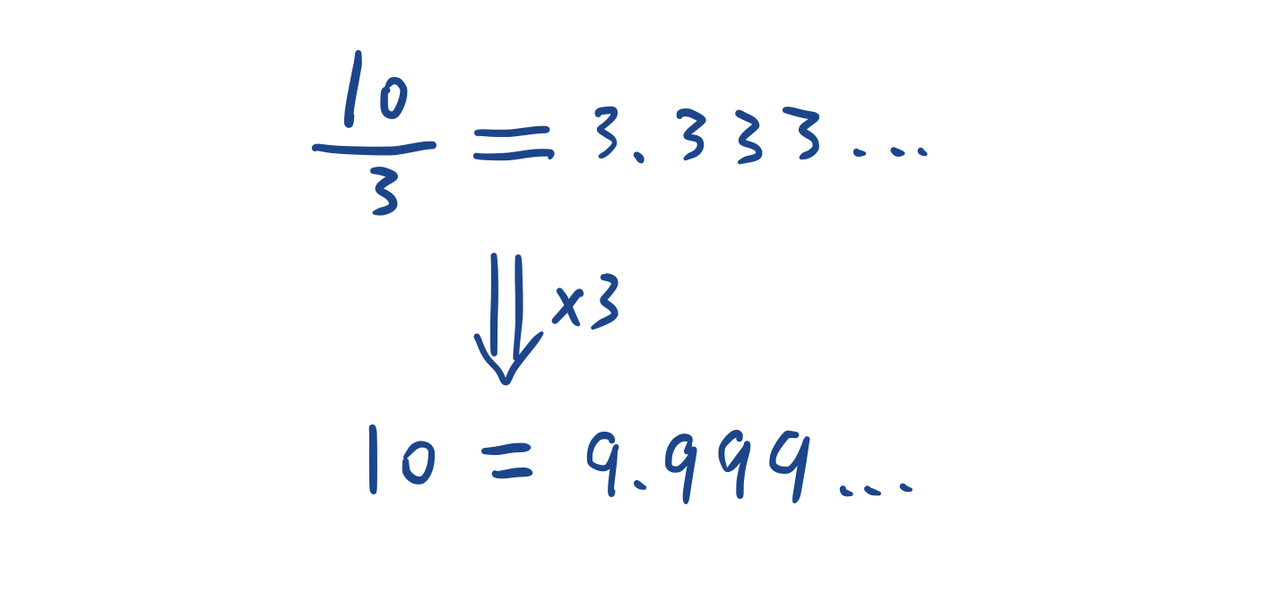
代数证明

有人会感觉怪怪的。为了增加可信度，这里用代数来证明。假设M = 9.999……，那么10M = 99.999……，两者相减得到9M = 90，因此M = 10。

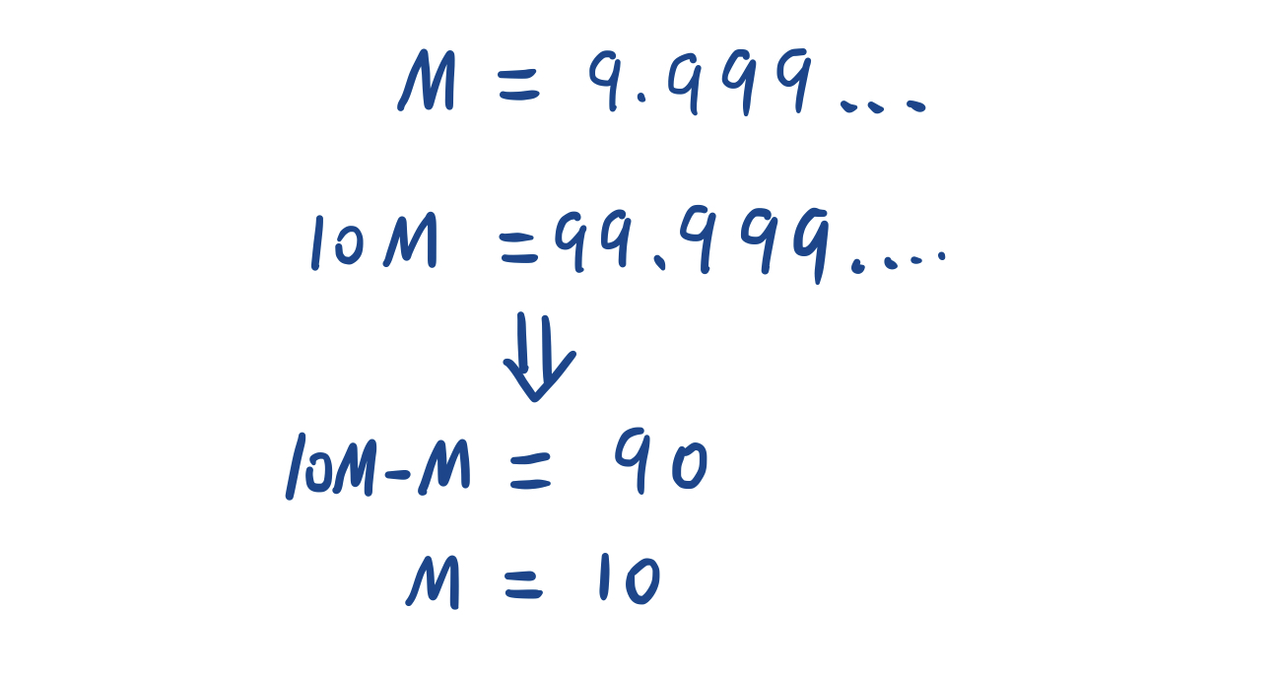
分数证明

上面的小数用得不规范，这里用分数给出更严格的证明，方法和代数证明相同：

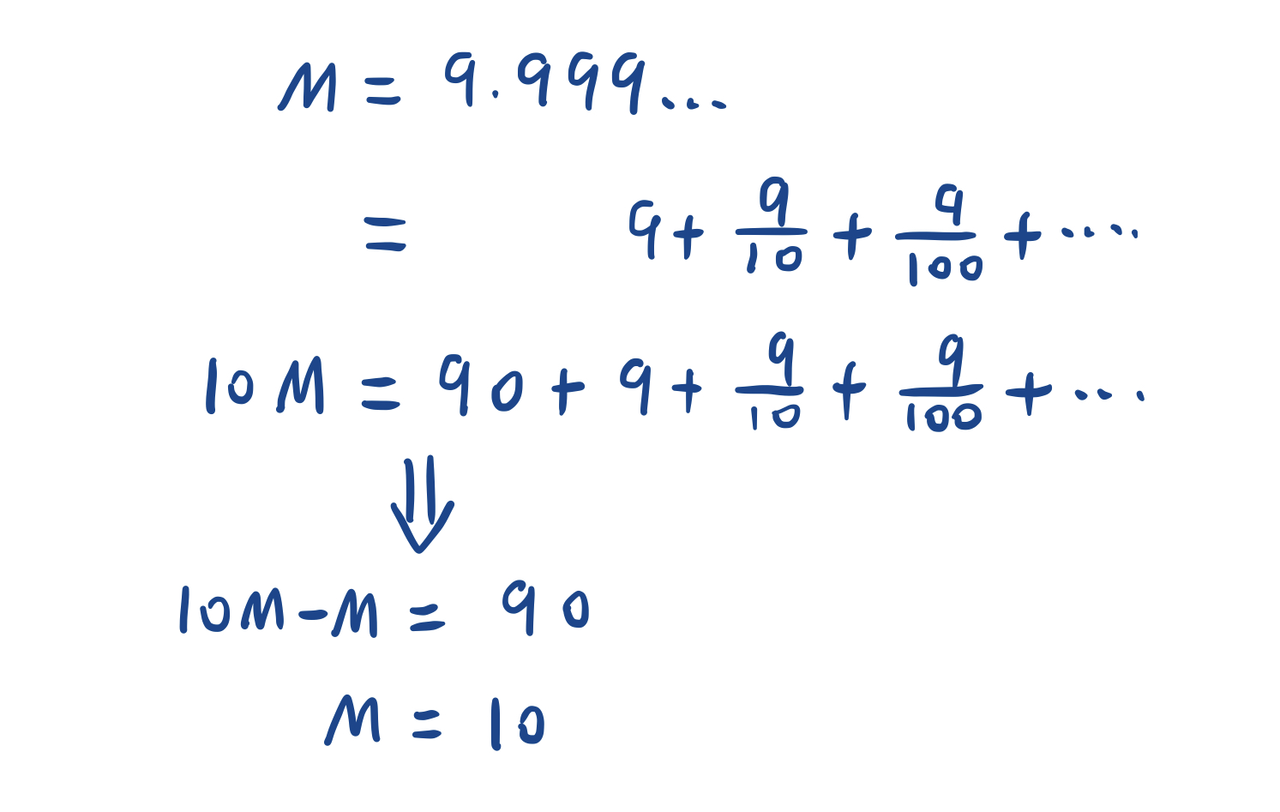
推广

Mathologer认为，这样的等式可以推广到任意的数字：

10 = 9.999……
128 = 127.999……
3.5 = 3.4999……

补充证明

Mathologer的证明还不够严谨，他将两个式子相减，却没有证明两个式子长度是否相等。如果两个式子长度不相等，相减就会有余项，让证明不成立。

我补充一个更严谨的证明：10可以分拆成两个有限的部分，一部分是9.99……9，另一部分是0.00……1，这两部分小数的长度都是N。当N趋于无穷时，第一部分成了题目中的无限循环小数9.999……，而后一部分无限趋近于0。取极限，原式成立。

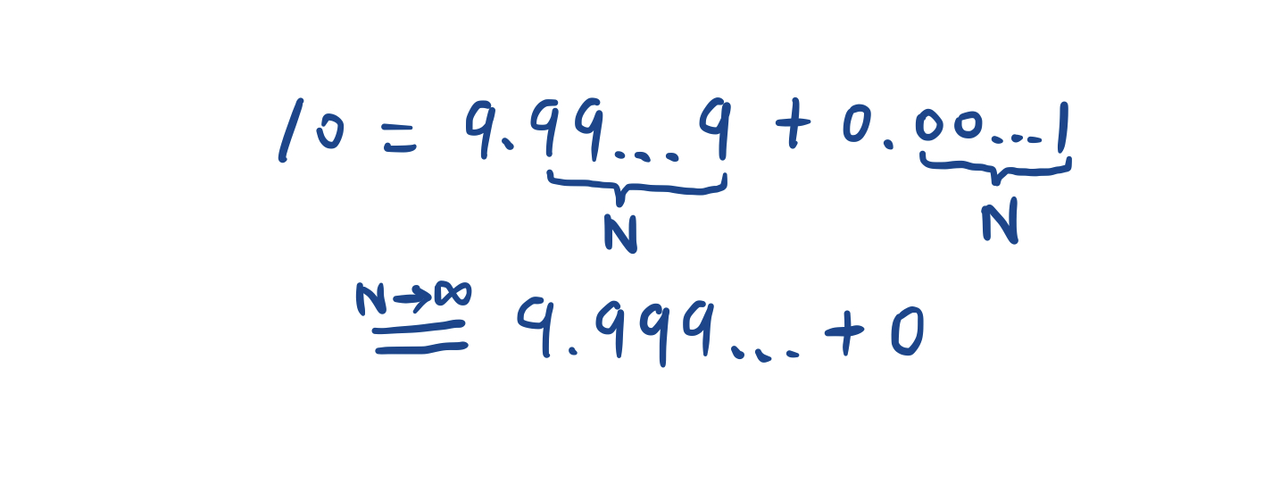
全文完